Calculez l’aire d’un triangle

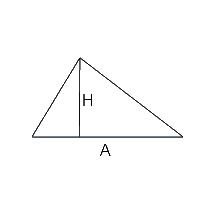
La définition du triangle

Un triangle est une figure géométrique composée de trois côtés. Ce polygone a la particularité de permettre différents calculs concernant les autres figures géométriques, c’est la science que l’on appelle la trigonométrie. 300 avant J.C., déjà Euclide dans son ouvrage Eléments d’Euclide, faisait la démonstration de l’importance du triangle dans la géométrie et dans les formules de calcul.

Les différents types de triangles

Il existe différents types de triangles qui répondent à des conditions géométriques bien distinctes. Le triangle quelconque ne possède aucun côté identique et n’est doté d’aucun angle droit. A l’inverse, le triangle équilatéral possède trois côtés de même longueur, ce qui lui confère automatiquement trois angles d’une ouverture de 60°. Le triangle rectangle quant à lui à la particularité de posséder un angle droit, c’est-à-dire un angle de 90°. Son nom vient du fait qu’il représente exactement la moitié d’un rectangle. L’on retrouve également le triangle isocèle qui comporte deux côtés égaux.

A noter que la somme des angles d’un triangle, qu’il soit quelconque, équilatéral, rectangle ou isocèle, est toujours égale à 180°, ce qui correspond à un angle plat.

Calculez l’aire d’un triangle

Pour calculer l’aire d’un triangle à partir de sa hauteur. La formule se présente comme suit : Aire = (base x hauteur) / 2. La hauteur est définie par l’angle droit qui la caractérise. Si le triangle n’est pas rectangle, c’est-à-dire qu’il ne possède pas d’angle droit, cette formule peut tout de même s’appliquer car un triangle quelconque, isocèle ou équilatéral peut être décomposé en deux triangles rectangles, à l’exception des triangles obtusangles, afin de déterminer précisément la hauteur. Pour les décomposer, il faut faire partir un segment depuis la base du triangle jusqu’à son sommet. Attention à ne pas vous référer à la longueur de la base et tenter de placer le segment au milieu. Cette droite n’a pas besoin d’être placée au centre de la base mais d’avoir un angle droit, et donc d’être tracée de façon perpendiculaire à la base.

Et pour un triangle obtusangle

Un triangle obtusangle est un triangle qui possède un angle obtus. C’est-à-dire que l’un de ses angles est supérieur à 90°. Il vient en opposition au triangle acutangle, désignant les triangles possédant trois angles aigus (moins de 90°). Le triangle acutangle possède donc trois angles aigus. Il est à noter qu’un triangle ne peut pas posséder plus d’un angle obtus, car en effet, la somme des trois angles doit être égale à 180°, c’est-à-dire à un angle plat. De même, un triangle rectangle ne peut jamais posséder aucun angle obtus. En effet, si l’on considère son angle à 90°, il est impossible que l’un des deux autres angles puisse se trouver supérieur à 90°.

La trigonométrie

La trigonométrie est une science mathématique qui définit et projette les liens qui peuvent exister entre ouverture des angles d’un triangle et longueurs des côtés. En découlent les fonctions trigonométriques telles que le sinus, le cosinus ou encore la tangente.

La triangulation

Les applications liées au triangle sont nombreuses, et la triangulation en est certainement l’une des plus fondamentales et des plus utilisées dans le monde. Cette technique permet, simplement en mesurant les angles d’un triangle, de déterminer avec exactitude un point donné. Cela permet de ne pas avoir à mesurer la distance entre les points ce qui peut être plus fastidieux et moins précis. Concrètement, le point se définit comme le sommet d’un triangle dont l’on connaît les deux valeurs d’angle et la longueur d’un côté. La triangulation est particulièrement connue pour repérer une position dans le monde maritime, et surtout lors de sauvetages.