Calcul de surface

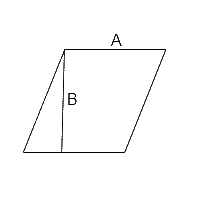
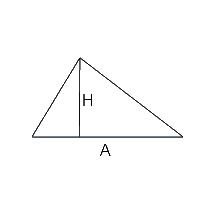
Les figures dont l’on peut calculer la surface

Voici les différentes figures géométriques dont l’on peut calculer la surface grâce à des formules simples :

• le carré se définit par ses quatre côtés égaux et ses quatre angles droits
• le rectangle possède deux côtés de même longueur et lui aussi quatre angles droits
• le parallélogramme possède lui aussi deux côtés de même longueur et parallèles mais il se différencie du rectangle par l’absence d’angles droits
• le triangle est formé de trois côtés, l’on distingue :
  • le triangle quelconque
  • le triangle équilatéral : trois côtés de même longueur
  • le triangle isocèle : deux côtés de même longueur
  • le triangle rectangle : qui possède un angle droit (le triangle rectangle est l’exacte moitié d’un rectangle)
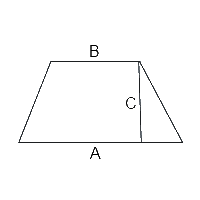
• le trapèze : qui possède deux côtés parallèles que l’on appelle bases
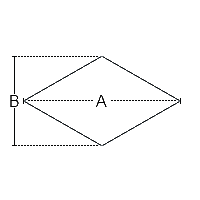
• le losange : comme le carré, il est doté de quatre côtés de même longueur mais il ne possède aucun angle droit
• le disque

Nous traitons ici des formes géométriques en deux dimensions et n’abordons pas les plus épineux polygones à trois dimensions comme la sphère, la calotte sphérique, le tore ouvert, ou le cône. Toutefois, si vous avez besoin de calculer ce type de surfaces, consultez le théorème de Guldin.

Les formules de calcul des surfaces

Maintenant que nous avons vu les formes géométriques existantes en deux dimensions, voyons les formules correspondantes au calcul de leur surface :

• pour le carré, la surface est obtenue en multipliant le côté par le côté, soit : surface = côté x côté ou encore surface = côté²
• pour le rectangle, l’on multiplie la longueur par la largeur, soit : surface = longueur x largeur
• pour le triangle, le calcul de l’aire se fait comme suit (en définissant la hauteur grâce à un segment partant à angle droit de la base jusqu’au sommet) : surface = (base x hauteur) / 2 (et comme l’aire d’un triangle est la moitié de celle d’un rectangle, l’on peut aussi poser la formule : (longueur x largeur) / 2
• pour le parallélogramme, la formule est la suivante : surface = base x hauteur (comme pour le triangle, l’on obtient la hauteur par une droite partant à angle droit de la base vers un des sommets)
• pour le calcul de la surface d’un trapèze, cela se corse légèrement, le calcul se fait ainsi : surface = [(grande base + petite base) x hauteur] / 2
• pour un losange, la formule est : surface = (diagonale 1 x diagonale 2) / 2 (la diagonale s’obtient en reliant les sommets opposés, sachant qu’elles se croisent à angle droit)
• enfin, pour le disque : surface = Pi x le carré du rayon ou surface = Pi x rayon² (le rayon s’obtient en mesurant le point central du disque jusqu’à l’un des côtés)

Pourquoi calculer une surface ?

Vous avez fini vos études depuis bien longtemps, et vous ne comptez pas intégrer Maths Sup à l’avenir, alors vous vous demandez à quoi peut bien servir de connaître toutes ces formules pour calculer la surface d’un polygone. C’est bien beau de briller en société, mais si cela ne vous est nullement utile, vous oublierez ces quelques formules aussi vite que vous les avez appris.

Calculer la surface d’une pièce

En effet, le calcul de surface s’avère très utile dès lors que l’on fait un peu de bricolage ou encore si l’on souhaite mesurer la taille réelle d’une pièce en mètre carré. Mais comment calculer la superficie d’une pièce ? La formule la plus souvent utilisée est d’ailleurs celle du rectangle, puisque l’on trouve le plus souvent des pièces de cette forme (pour rappel, on calcule la surface d’un rectangle en multipliant la longueur par la largeur de la pièce). Mais n’oubliez pas non que toutes les pièces ne sont pas rectangulaires et que si cette dernière est carrée ou trapézoïdale, il faudra adapter votre formule en vous en référant aux exemples ci-dessus.

Dans les faits, le calcul de surface d’une pièce peut donc vous être utile pour :

1. Calculer le nombre de mètres carrés de carrelage au sol ou de parquet à acheter ;
2. Identifier la superficie de chaque pièce lors de la vente de votre bien ;
3. Réfléchir à l’aménagement de votre pièce en fonction de sa superficie (il existe notamment de nombreux exemples d’aménagement et de décoration pour une salle de bain ou une chambre en fonction de la surface ; l’organisation de la pièce n’est en effet pas le même et vous verrez qu’un ou deux mètres carrés dans une salle de bains par exemple peut changer beaucoup de choses).

Dans l’absolu toutefois, et même si vous n’êtes pas bricoleur, les calculs de surfaces se trouvant au programme des classes de collège, vous serez certainement fier de pouvoir aider vos enfants à y voir plus clair dans ces méandres géométriques. Car si vous ne connaissez pas vos classiques, il y a peu de chances qu’eux trouvent un quelconque intérêt à les apprendre.