- Actus
- Mathématiques
- Calcul du volume d'un cylindre
Calcul du volume d’un cylindre
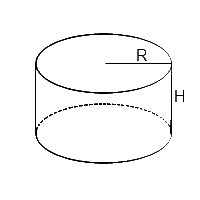
Le volume du cylindre
La formule de calcul du cylindre est simple, elle se résume à (mais attention car elle n’est pas la seule) : volume = aire du cercle x hauteur. Comme nous l’avons vu, le cylindre comprend deux cercles identiques et parallèles à sa base et à son sommet. Dans cette formule, il est tout d’abord important de connaître l’aire du cercle dont nous parlons. Ainsi, pour parler concrètement prenons un exemple pratique. Imaginons un cylindre en volume, dont la hauteur est de 10 cm, et le rayon du cercle est de 3 cm. Ce rayon, comme vu sur notre page pour calculer l’aire d’un cercle, est obtenu en reliant le point central du cercle à un point A donné sur la circonférence de la figure. Ce point central, O, donne donc AO comme rayon du cercle. Il est exactement la moitié du diamètre puisque deux points placés sur le cercle, A et B, reliés par un segment qui passe par O, nous donne le diamètre. Ainsi l’on comprend qu’AO et OB sont identiques, il s’agit du rayon r. Par conséquent, le diamètre représenté par le segment AB est le double de r.
Commençons par calculer l’aire du cercle. Nous savons que la formule pour obtenir l’aire du cercle est : aire = pi x rayon². Ainsi donc, dans notre cas, l’aire du cercle (indifféremment celui de la base ou du sommet du cylindre) est de :
- aire = pi x rayon²
- A = 3,14 x 3²
- A = 3,14 x 9
- A = 28,26 cm²
Maintenant que nous connaissons l’aire du cercle ainsi que sa hauteur, nous pouvons poser la formule :
- volume = aire du cercle x hauteur
- V = 28,26 x 10
- V = 282,60 cm³
Le volume de notre cylindre est donc de 282,60 cm³. A noter que nous avons pu procéder facilement à ce calcul car les données, l’aire du cercle ainsi que la hauteur du cylindre, sont exprimées dans la même unité de longueur, à savoir le centimètre. Si ces nombres avaient été exprimés dans des unités différentes, il aurait été nécessaire de procéder à une conversion avant de pouvoir appliquer la formule.
Et sans connaître l’aire du cercle ?
Pour calculer le volume d’un cylindre, une autre formule existe, et elle fait aussi intervenir le nombre pi, tout comme il intervient dans le calcul de l’aire du cercle. Cette formule permet d’éviter par la phase de calcul de l’aire du cercle et se présente : volume du cylindre = pi x rayon² x hauteur. L’on voit que tout simplement, la valeur de l’aire du cercle s’est décomposée en : pi x rayon². Ce qui est sa formule de base. Elémentaire et évident. Alors toujours avec notre cylindre de 10 cm de hauteur et de 3 cm de rayon, nous allons vérifier notre calcul de volume précédent :
- volume du cylindre = pi x rayon² x hauteur
- V = π x r² x h
- V = 3,14 x 3² x 10
- V = 3,14 x 9 x 10
- V = 28,26 x 10
- V = 282,60 cm³
Nous retrouvons bien le même résultat qu’avec la formule précédente, à savoir que le volume du cylindre dont nous parlons est de 282,60 cm³.
A noter, que le sens de l’opération de multiplication n’a aucune incidence. En effet, que l’on fasse :
- (3,14 x 9) x 10
- 28,26 x 10
- 282,60
Ou que l’on fasse :
- 3,14 x (9 x 10)
- 3,14 x 90
- 282,60
L’on obtient le même résultat.
Avec nous, vous calculez le volume d’un cylindre simplement.
Cas concret : le volume d’un vase
Sur notre site, vous savez que nous aimons rattacher les formules et les principes mathématiques à des cas concrets du quotidien. Il est en effet toujours plus agréable de savoir que la formule nous sera utile un jour et on la retiendra ainsi plus facilement.
Si l’on rentre donc un peu dans le concret, amusons-nous à calculer le volume d’un vase artisanal de forme cylindrique.
Tout va déjà dépendre de la forme du vase en question : s’agit-il d’un cylindre simple ou d’un cylindre avec une demi-sphère sur le dessus ? En fonction de la forme, vous aurez en effet besoin d’utiliser uniquement la formule du calcul de volume d’un cylindre, ou d’ajouter également le calcul du volume de la sphère additionnelle.
Dans le cas où le vase est accompagné d’une demi-sphère, le calcul de son volume sera alors :
- volume vase = volume du cylindre + volume demi-sphère
Sachant que le volume d’un cylindre = π x r² x h et que le volume de la sphère = 4/3 x π x r3
Cela nous donne donc :
- volume vase = (π x r² x h) + (4/3 * π * r3)/2
Cela vous permettra de connaître le volume maximum d’eau que le vase peut contenir.
En complément de lecture, nous vous proposons les articles suivants: